Gas Chromatographs for Education and Industry
Basic principles of gas chromatography
Chromatography in the gas phase is one of the cornerstones of instrumental analysis. After rapid development in the Seventies and Eighties of the last century, this technique has now, with the help of digital electronic and data processing, established itself on a highly advanced level. Suitable for all mixtures which can be vaporised without resulting in chemical changes, it even allows the separation of complex mixtures of substances in very small portions. In many cases, the retention times can be used to identify individual components; the peak areas allow quantitative determination after calibration.
Principle of operation
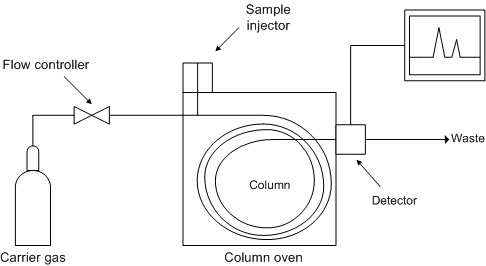
The operating principle of a gas chromatograph (Wikipedia)
An inert carrier gas, usually hydrogen or helium, flows in succession through a pressure control unit , injector, separation column and detector . The mixture to be separated is introduced into the heated sample injector with a microlitre syringe and vaporised there. The gaseous components of the mixture are transported by the carrier gas into the column and subsequently into the detector. The column separates the gaseous components spatially by retaining them for differing periods. As a result, these components emerge from the column at different points in time. When a component of the mixture emerges from the column, the detector issues an electrical signal which is recorded as a function of time. Earlier, this was done using a laboratory recorder; nowadays, the signal is converted into digital form and stored on standard media (e.g. hard disks or flash memory).
The chromatographic separation principle
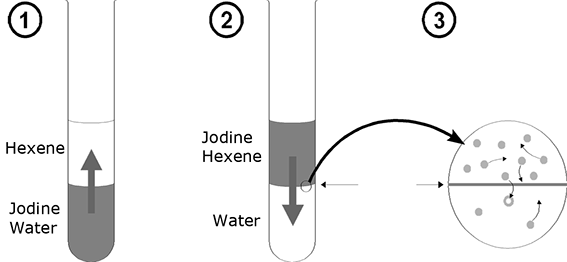
1. Distribution
The process of distribution is best elucidated by means of a small experiment. A few crystals of iodine are added to a potassium iodide solution having a concentration c = 1mol/l. When shaken, the iodine crystals dissolve, turning the solution brown. If the solution is overcoated with a layer of hexane, the iodine particles diffuse through the phase limit into the hexane, turning it violet. After that, the experiment is performed in reverse order. A small quantity of iodine is dissolved in hexane and undercoated with a potassium iodide solution. This time, the iodine diffuses from the alkyl phase into the aqueous phase. Both these initial situations classically result in a dynamic equilibrium. If one waits long enough in both cases, the number of particles crossing the phase boundary from "top" to the "bottom" and vice versa turns out to be identical per unit of time, i.e. the concentration of particles remains unchanged over time in both phases.
According to NERNST, the following equation applies to small values of c in this case:
c(iodine in phase 1) / c(iodine in phase 2) = const
Consequently, the ratio of concentrations is a constant. This value is also termed distribution coefficient.
2. Distribution in the case of mobile phases
In an imaginary experiment, several test tubes of the type shown above are now arranged consecutively, but it is additionally assumed that one of the phases is laterally movable (mobile phase) while the other one remains fixed (stationary phase). In addition, the mobile phase is assumed to be slow in comparison with the diffusion rate.

This imaginary experiment provides several results:
• The particles in such a system drift with the mobile phase, but more slowly, because they are only moved by the phase when they are actually in it.
• The range over which the particles to be separated drift through the column increases during the course of the experiment.
• The speed of the particles relative to the mobile phase is directly dependent on the distribution coefficient, because statistically, a particle present more often in the stationary phase remains at rest longer. For this reason, its average speed is less than that of a particle which is present more often in the mobile phase. The relative speed of the particles is thus dependent on the substances involved with the result that it can be used for analytical separation.
The distribution coefficient is strongly dependent on the temperature. This can be easily understood in mechanochemical terms, because as the temperature increases, so does the drift rate of the particles and, consequently, their tendency to remain in the gaseous state (where the entropy is higher). This property is frequently made use of in chromatography.
If the components in a mixture to be separated have widely differing boiling points, it might not be possible to separate all the individual substances given a constant column temperature. Either the substances with higher boiling points take a very long time to emerge from the column (elution) when the column has a low temperature, or the substances with lower boiling points are not separated when the column has a high temperature. This can be remedied by programming the temperature of the column furnace.
In practice, measurements are usually commenced at a column temperature matched with the most volatile component. After a phase of constant temperature (t0-t1), the column temperature is made to increase linearly over time (t1-t2) to allow elution of the less volatile components from the column. After this linear heating phase, the temperature is usually adjusted back to a constant level (t2-end). This type of temperature programming for the column furnace is a widely used technique nowadays. Figure below shows a standard temperature program. The heating rate dT/dt is stated in degrees/minute; values here typically lie between 1 and 10 K/minute.

Home
Contact us
Legal Notice